こんにちは。和からの数学講師の岡本です。今回は「整数の分割」という素朴な話題についてお話いたします。例えば、「3」という整数は「1+1+1」や「1+2」など、「3」自身を含めて全部で3通りの表し方があります。「整数の分割」の主な興味はこの分割の種類を考えることになります。
この記事の主な内容
1.分割数を考える
先の例であったように、「3」という整数は正の整数を使って3通りで表すことができます。このような場合の数を「分割数(partition number)」と呼び、p(3)=3と表現します。実際に小さい数から分割数を計算してみましょう。「1」は1通りなのでp(1)=1、「2」は「1+1」とも会わらせるのでp(2)=2。そして「4」に関しては
4=3+1=2+2=2+1+1=1+1+1+1
となり、全部で5通りの表し方があります。したがってp(4)=5となります。続きは以下のようになります。
p(5)p(6)p(7)p(8)p(9)p(10)=7=11=15=22=30=42
何か規則が見えてきましたか?
2.分割数の歴史
先史時代から、人類はものを数えるのに木や石、絵などを使っていました。例えば、石を3つ並べると「3」を意味します。しかし、下の図のように並び方を変えると【「2」と「1」の合計】と捉えることもできます。
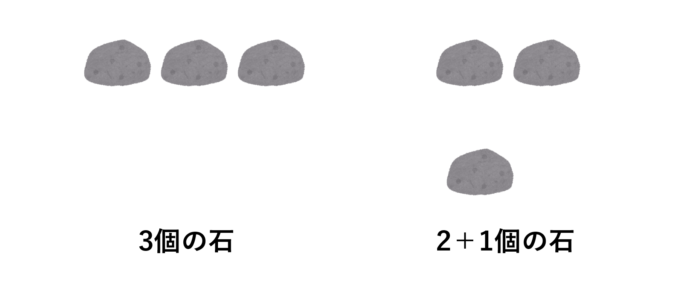
さらに次の図をご覧ください。
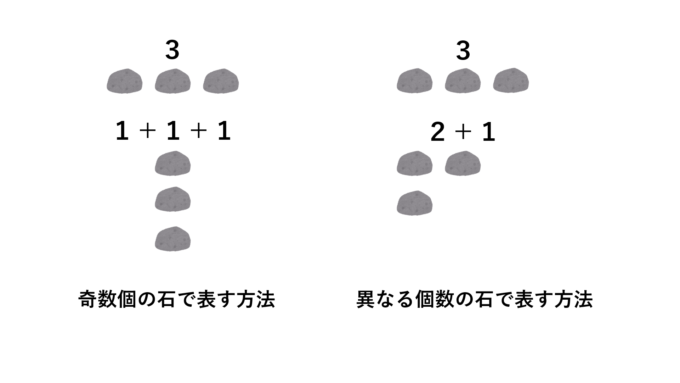
4個の石に対しては次にようになります。
左には奇数個の石だけで表現する方法を表し、右には異なる個数の石で表現する方法を表しています。
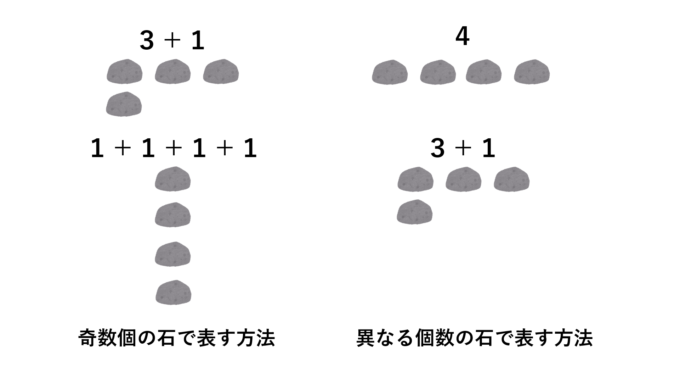
4個の石に対しては上のようになります。続きを数字を使って表にしてみました。
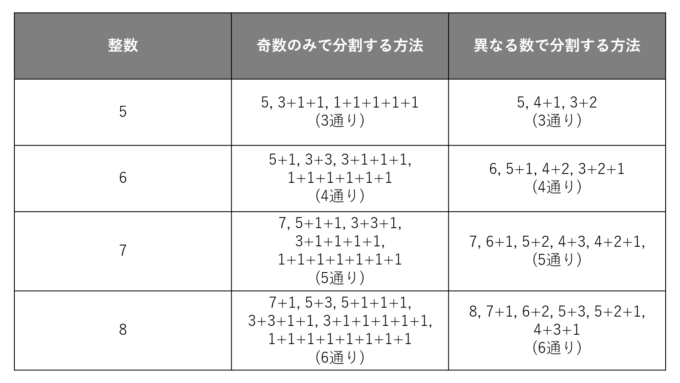
この表から予想できるかもしれませんが、実は左のような「奇数のみで分割する方法」の数と「異なる数で分割する方法」の数は常に一致します。この事実は1748年にかの有名なレオンハルト・オイラーによって最初に証明されました。
【奇数のみで表す分割方法】の総数=【異なる数で表す分割方法】の総数
オイラーに関する記事は以前マスログで取り上げたので興味のある方は是非ご覧ください。
なお、オイラーが示した主張を数式で表したものが以下の等式になります。
∏n=1∞11−q2n−1=∏m=1∞(1−qm).
上のような分割数に関する等式は他にもたくさん知られており、1894年にはロジャースによって、また1913年にはインドの天才数学者ラマヌジャンによって独立に以下のような新しい事実が発見されました。
【5で割って1または4余る整数たちで表す分割方法】の総数=【差が2以上の数で表す分割方法】の総数
かなりマニアックな性質ですが、現在では“ロジャース・ラマヌジャン恒等式”と呼ばれ、今もなお多くの人を魅了する美しい理論と結びついています。なお、このほかの分割数に関する有名な話題として「オイラーの五角数定理」とうものがあります。実は岡本が大好きな定理の一つであり。以前、マスログの記事にしています。興味のある方は是非こちらも併せてご覧ください(※数式多いので閲覧注意)。
3.ロジャース・ラマヌジャン恒等式
せっかくなのでロジャース・ラマヌジャン恒等式の具体例を考えてみましょう。まず、「5で割って1または4余る正の整数」というのは具体的にA={1,4,6,9,11,14,16,19,21,…}という集合の元です。簡単にいうと1の位が1,4,6,9となる数たちです。例えば、「5」という整数は上の数のみを使って「1+4」と表せます。このほかに方法はないので、上の数を使った分割方法は1通りとなります。また、差が2以上の数で「5」を分割しようとすると「1+4」以外にあり得ないので、やはりこの方法でも1通りとなり、ロジャース・ラマヌジャン恒等式が確かめられました。
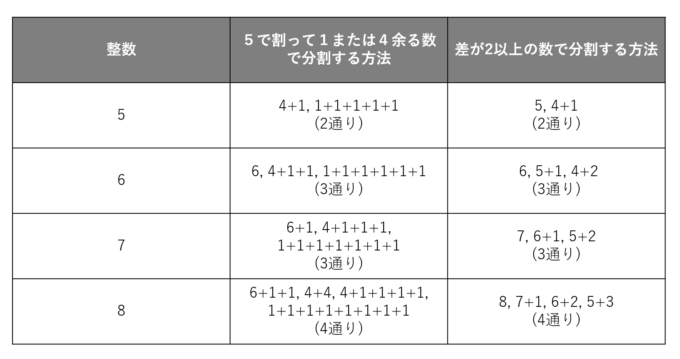
次に「6」について考えてみましょう。「6」はAの元を使って「6」,「4+1+1」と2通りで表せます。また2以上差のある数での分割としては「5+1」, 「4+2」の2通りのみです。「7」の分割を考えましょう。Aの元では「1+1+1+4」,「1+6」の2通りであり、2以上差のある数では「1+6」, 「2+5」の2通りです。どれもロジャース・ラマヌジャン恒等式を満たしていることがわかります。
ちなみに、ロジャース・ラマヌジャン恒等式を表す美しい等式を提示しておきます。
∏n=1∞1(1−q5n−4)(1−q5n−1)=1+∑m=1∞qm2(1−q)(1−q2)⋯(1−qm).
記号の意味は省略しますが、ロジャース・ラマヌジャン恒等式の成立は上の等式の成立と同等であるという美しい帰結を目で見て味わっていただければ幸いです。
4.分割数の挙動
第1節に分割数p(n)の例を書きましたが、実はこの規則はそんなに簡単なものではないことが知られています。1918年にハーディとラマヌジャンにより以下のような漸近的な表示が示されています。
定理(ハーディ,ラマヌジャン(1918))
nが十分大きいとき、p(n)の挙動は
f(n)=14n3–√eπ2n3√
に近づく。
意味が分からないほど複雑な式は出てきました。円周率π、ネイピア数e!分割数は恐ろしくポテンシャルを秘めたものだったようです。
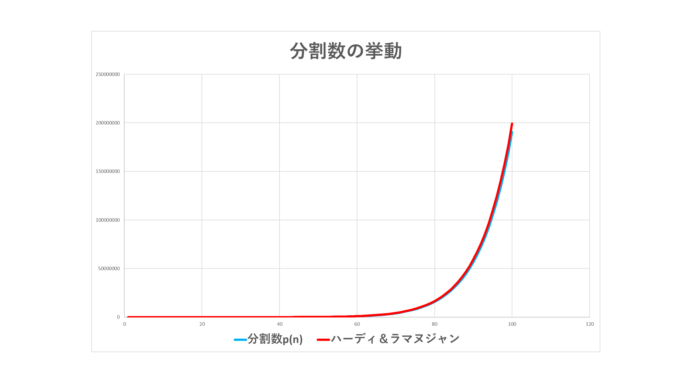
なお、上のグラフは分割数p(n)とハーディとラマヌジャンによって得られた関数f(n)の挙動をn=1~100までグラフにしたものです。非常に近い曲線になっていることがわかります。
5.分割数と素数
分割数に関してはその他にも様々な性質が見つかっています。例えば、ラマヌジャンによって【「5で割って4余る数」の分割数は5で割り切れる】ということ発見され、続けて【「7で割って5余る数」の分割数は7で割り切れる】【「11で割って6余る数」の分割数は11で割り切れる】といった衝撃の事実も発見します。
確かにp(4)=5,p(9)=30なので、どちらも5で割れます。またp(5)=7,p(12)=77なので、確かに7で割り切れます。さらにp(6)=11,p(17)=297=11×33なので11で割り切れます…。恐るべき、分割数、そしてラマヌジャン…!
4.さいごに
いかがでしたでしょうか?今回は分割数という、ややマニアックですが、ものすごく奥の深い理論のさわりだけお話してみました。この機会にぜひ「分割数」というものを覚えていただければ幸いです。なお、分割数に関するオススメの書籍はアンドリュース&エリクソンの「整数の分割」が有名です(訳書もでています)。
和からでは「分割数」について上記の本を使って個別レッスンを受けることも可能です!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>