この記事の主な内容
微分トポロジー
数学の分野には大きく分けて、解析(微積分や関数)、幾何(図形や空間)、代数(方程式や群)とありますが、トポロジーは「位相幾何」とも言い、幾何学の仲間で「空間全体の大域的な様子」を研究します。そのための道具としては、解析、代数、幾何など何でも使います。
トポロジーで研究の対象としている空間を「位相空間」と言い、中でも、どこもかしこも局所的にはユークリッド空間(平面や3次元空間など)と同じ、つまり「普通」に見える位相空間を「多様体」と言います。「多様体」のうち、「つながり方」だけに注目する「位相多様体」に対して「無限回微分可能な程度の滑らかさ」を要求するのが「滑らかな多様体(可微分多様体とも)」です。よって、滑らかな多様体には尖った角などは一切なく、どこでも通常の座標空間と同様に微分や積分の計算ができます。至る所ギザギザかもしれないような位相多様体に比べ、より現実味があり物理学や工学等での応用上もよく出現します。
「微分トポロジー」とは、このような「滑らかな多様体」を調べる数学の分野です。
球面の裏返し
微分トポロジーでは、2つの滑らかな多様体の間に「微分同相写像(滑らかさを壊さないようにそっと移す写像)」があるとき、「つながり方も滑らかさも同じ」という意味で同型とみなします。ですから、微分トポロジーでの「変形」は、単につながりを保っていればよいだけではなく、「途中で折り曲げたりせず、滑らかさを保って」行う必要があります。
このことの意味は、平面内の円周を、平面から持ち上げずに、逆向きにするには、少なくとも1か所を必ず折り曲げなければならない、ということを考えてみるとわかるかもしれません。(向きの異なる2つの円周は2次元空間内の滑らかなはめ込みの変形でつながらない、ということ)。
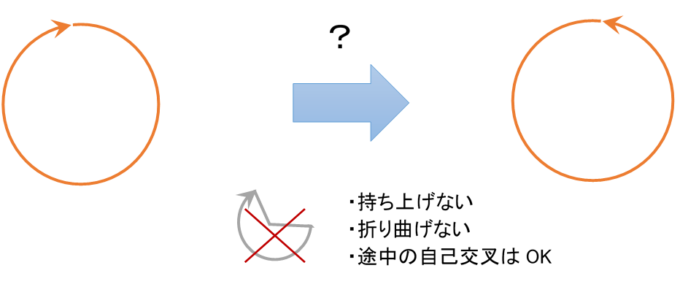
一方、球面は3次元空間内で一切折り曲げずに裏返すことができます!
エキゾチック球面
3次元以下では、各位相多様体(の同型類)の「滑らかさ加減」というのはそれぞれ1つずつしかないのですが、4次元以上ではそうとも限りません。例えば7次元には、7次元球面S7に位相同型だけれども微分同相ではない多様体が28種類も(!)あることが、1956年以降ミルナーらによって発見されました。これらの通常と異なる滑らかさを持つ高次元球面は「エキゾチック球面」と呼ばれています。ちなみに、各次元の球面の可微分構造は、以下の表のようになっています。(「球面」と言っていますが、実際には各次元の広さ(自由度)を持つ、境界のない閉じた空間のことを指しています)
https://en.wikipedia.org/wiki/Exotic_sphere
| 球面の次元 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 滑らかさの種類 | 1 | 1 | 1 | ? | 1 | 1 | 28 | 2 | 8 | 6 | 992 | 1 |
4次元は特別?
また、4次元座標空間(R4)には通常と異なる滑らかさの構造が連続的にたくさんある(エキゾチックR4)ことがフリードマン、タウベスらにより証明されています。これはn=4だけの特性で、n≠4ではRnの滑らかさは通常の1通りしかありません。(Rnとは、n次元の自由度を持つ、閉じておらず境界もない空間をイメージしてください)
「参考)エキゾチックR4(wikipedia)」
このように4次元空間は何か特別、謎めいています。これは私たちの住む時空が、空間3次元、時間1次元の4次元であることと関係があるのでしょうか。でも超弦理論によれば、本当の世界は10次元や11次元なんだとか。隠れた7次元はエキゾチックなのかも、などと想像は膨らみます。ちなみにトポロジーでは高次元とは5次元以上を指し、4次元の世界は「低次元」のうちに入ります。
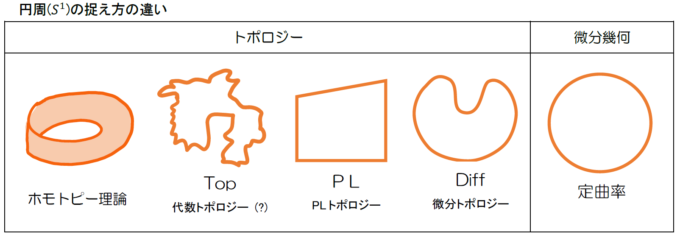
3つのカテゴリー
トポロジーには、TOP(位相多様体)、PL(組み合わせ多様体)、DIFF(可微分多様体)の3つのカテゴリーがあり、それぞれのカテゴリーごとに多様体を分類することを目標のひとつとしています。さらにそれらの下に「ホモトピー論」というカテゴリーがあります。その観点で「一般化」ポアンカレ予想を言い換えると、「ホモトピー型がn次元球面と同相(PL同相、微分同相)なn次元閉多様体は、n次元球面に同相(PL同相、微分同相)か?」となります。ポアンカレ予想はペレリマンによって最終的にすべて解決された、と言われていますが、実はこれはTOP(位相)カテゴリーの話で、2021年現在でも唯一、4次元のDIFF(微分)カテゴリーのみが未解決で残っています。つまり、滑らかで単連結な4次元閉多様体があったとき、それは必ず通常の4次元球面S4に同相(位相同型)になることは分かっているが、微分同相か(滑らかさを保つ写像か)どうかはわからない、ということなのです。
「参考)Generalized Poincaré conjecture(wikipedia)」
参考動画
数学を創る-数学者達の挑戦(東京大学学術俯瞰講義)2009年度
https://ocw.u-tokyo.ac.jp/course_11323/
↑ 第10回~第12回で幾何学やトポロジーを解説しています。
①次元(数学の散歩道)第1章~第9章
http://www.dimensions-math.org/Dim_JP.htm
②カオス(数学的冒険)第1章~第9章
https://www.chaos-math.org/ja.html
①②とも、日本語版吹き替えと字幕があります。
<文/佐々木和美>
