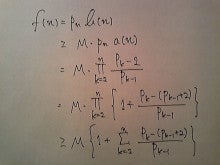※4/2 1:10追加※
コメ1にある通り、5.で間違いがありました。ご指摘有難うございます。
一応、この記事自体は(一部改編してますが)残しておきます。証明は全て元の通りおいてあるので、他にも誤りがあれば指摘をお願いします。
数式をここに書くのは面倒だし嫌なので(と言うかできるかも不明ですが)、概略のみ書いてあります。
途中式がどうしてもわからんと言う人がいれば、適宜写真を貼るなりしていきますので、指摘して下さい。
以下証明
1. 言葉の定義
n番目の素数をp(n)で表わす(写真等でアップする際には、p(n)のnは添え字で書きます)
「p(n)-擬似双子素数」でp(n)以下の全ての数で割り切れない数、または素数の組で、差が2の自然数組を指す(必要があればp(n)-s.t.p.などで略す)
例えば(47,49)はp(3)-s.t.p.であり、(11,13)は任意の自然数nに対してp(n)-s.t.p.である
「割合」という単語を定義する
自然数(組)の性質Xに対し、Xの割合がaであるとは、
[n以下で、Xに当てはまる自然数(組)の個数] / n → a (n→∞)のコトを指す
例えば素数の割合は0であり、双子素数の割合も0である。2の倍数の割合は1/2である。
証明には、中国式剰余定理を用いればよい(ここでは略する)
以下、上の割合の式をa(n)で表わす
3. 準備
p(n)までのp(n)-s.t.p.の個数をf(n)で表わす
(f(n)は、p(n)までの双子素数の個数に等しい)
f(n)/p(n)をb(n)で表わす
4.補題2
任意のnに対してMa(n)≦b(n)なる実数Mが存在するとき、双子素数は無限個存在する
双子素数が有限であると仮定すると、有限個のkに対して
p(k)-[p(k-1)+2]=0
であり、それらを除いたkに対してp(k)-[p(k-1)+2]>1
Σ(1/p(k)) = ∞より、f(n)→∞(n→∞)を得る
これは矛盾
よって、双子素数は無限個である
5. 双子素数が無限個存在するコトの証明
双子素数を有限個と仮定すると、任意のnに対してMa(n)≦b(n)なる実数Mの存在が導かれるコトを示す
これによって、補題2より双子素数は無限個存在するコトが導かれる
双子素数が有限であると仮定すると、最大の双子素数組(p(N-1),p(N))が存在する。
n≧Nではf(n)が一定なので
b(n+1) = [p(n)/p(n+1)] b(n)
a(n+1) = [(p(n+1)-2)/p(n+1)]a(n)
従って
b(n+1)/a(n+1) < b(n)/a(n)
以上より
M = max b(k)/a(k) (k≦N)
とおけば、任意の自然数nに対してMa(n)≦b(n)なる実数Mが存在する ……(*)
以上
上の証明の誤り
(*)部についてコメ1参照
※4/2 1:30追加※
双子素数が有限と仮定した場合inf b(k)/a(k) = 0になるコトを確認したので、単純に補題2を用いて証明とはいかないようです。別の補題を用意するなり何なりしないとダメですね。
簡単にですが解説しておくと、a(k)はΠp(k) (k=1~n)程度の数に対して成り立つ"割合"で、b(k)を用いているのはその"割合"をp(k)程度にまで落とせるかと言う話です。