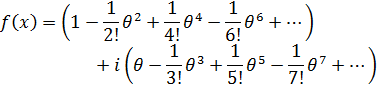■ 「複素数」に関する知識を強化する!
普段の生活には全く縁がないと思われる数学知識ですが、市場分析という
世界に足を踏み入れたのであれば無関係とは言えない知識になるでしょう。
でも今更学生時代の教科書を引っ張り出すには・・ (ノ_・。)
あ~微分って難しくてわからなかったなぁ・・
と知識の取得を諦めてしまう方も多いことでしょう。当コンテンツは、そんな方々
へお贈りいたします。
■ 今回扱う知識以外に必要な知識
■ 今回扱う知識は「オイラーの公式」
【物理数学の基本となるオイラーの公式】
今回は解説するオイラーの公式は物理数学において非常に重要な役割を
担う公式です。この公式を知っていることで様々な技術を習得できるといっ
ても過言ではありません。
そしてオイラーの公式は非常にシンプルで導出も決して難しいものではな
いのです。必要な知識は、
・ 三角関数 参考 : 三角関数の基礎
・ 指数関数 参考 : 指数関数とは?
・ 微分 参考 : あらゆる関数の微分
・ 高階微分 参考 : 高階微分とは?
・ テイラー展開とマクローリン展開 参考 : テイラー展開とマクローリン展開
・ 虚数 参考 : 虚数「 i 」の計算
となります。導出プロセスを簡単に示していきますのでオイラーの公式が
どのように構成されているかを覚えておきましょう (^O^)/
【SinとCosのマクローリン展開を行う】
まずテイラー展開とマクローリン展開の公式を載せておきましょう。テイラー展開
は、ある関数の高階微分に対して
x に a を代入
したものを展開の式に当てはめていくことでした。マクローリン展開は代入したa
に0を代入したものです。展開式としては、
となります。とりあえずSinXのテイラー展開を行いましょう。最初にSinXの高階
微分を計算してaを代入しておきます。
一応元のf(x)を綺麗に表示しましょうか (;^_^A
以下aを代入した高階微分の結果を示します。
これをテイラー展開の f(a)部分の当てはめていきますと下記のようになり
ますので確認してみてください。結構面倒な作業なのでCosは省略しますが、
基本的に同じプロセスです。Cosはマクローリン展開の結果だけ載せます。
そしてマクローリン展開は a に0を代入します。ちなみにSinのaに0を代入
しますと0になり、Cosのaに0を代入すると1になります。これは三角関数の
基礎知識ですね (^-^)/
そうしますと上記の式はスッキリした形になって・・・
こんな形になりました。これがSinのマクローリン展開になります。ちなみに
Cosのマクローリン展開は、
となります。この2つの展開結果を覚えておいてください。後からあっと驚く
ことになると思います o(^▽^)o
【 iθ における指数関数】
ここでは指数関数のXに iθ を代入することをします。まず指数関数は
下記式で表されますね (^-^)/
そして単純にXに iθ を代入しますと、
となります。当然のことながら代入するだけでは意味がありません。ただ、
この代入が意味するところは、複素数としての指数関数ということなのです
ねえ。これを計算したい場合はSinとCosで行ったテイラー展開とマクローリン
展開をする必要があります。では次項にて行いましょう (^O^)/
【iθ における指数関数のマクローリン展開と変形】
指数関数は微分しても形が変わらないので簡単です。基本的に通常の指数
関数のテイラー展開とマクローリン展開と変わりがないので手抜きで申し訳
ありませんが下記記事を参照してください。
参考 : 指数関数のテイラー展開とマクローリン展開
そしてマクローリン展開の結果は下記のようになります (^-^)/
虚数部分が計算できるので計算してみますと・・・
となりますね (^-^)/
虚数と実数に分かれたのでまとめてみましょうか o(^▽^)o
まとめてみると何か気づきませんか?
そうですSinとCosのマクローリン展開の結果と似ていますねえ Σ(゚д゚;)
ただ、SinとCosのマクローリン展開の結果はXなのでXにθを代
入しますと・・・
まとめたカッコの内部と完全に一致しますね ('-^*)/
ということで、
と表現されるオイラーの公式が導出されたのであります (ノ´▽`)ノ
ちなみにθをπに置き換えますとCosは-1となりSinは0になるので、
と表されることもあります。最も美しい等式とも呼ばれてますね o(^▽^)o
【オイラーの公式を考察】
オイラーの公式は複素解析を初めとする様々な分野で重要な役割を担いま
す。一見公式の意味が分からない感じもしますが、幾何学的に考察すれば、
複素平面における円を表しています。
そもそも極形式を思い出せばオイラーの公式のイメージも自然と湧いてくる
と思います。
参考 : 極座標形式
この円をクルクルしているイメージは大切です。下図はウィキペディアから拝
借したイメージ図ですが、このようにイメージしておくと良いでしょう (・∀・)
【次回への布石】
オイラーの公式の導出は難しいものではないと思います。記事にするのは
大変でしたが・・( p_q)
複素数の基礎に関しては大半が終えています。基礎としての最後に1つの
公式を次回にて紹介しましょう。後は複素数に関する応用になりますが、こ
の応用は必要に応じて追加していこうと思います。
複素数を知ることで様々な分野において登場する複素数への拡張という内
容が何となく理解できるようになります。何となくというのは、
複素数の計算における複素数の挙動を把握しないといけない
からです。これはグラフや応用されている数式から学ぶのが近道ですが、
その辺りまで来ますと極端に難しくなります。まずは複素数の計算を含んだ
様々な基本的な技術を習得することが先決でしょう。
概念としては負の値よりも難しいですが興味を持たれたら書籍などを購入し
て勉強すると良いと思います (^-^)/