封筒のパラドックス(7回目)
---------------------------------------------
封筒のパラドックス その4
---------------------------------------------
2つの封筒があり、1つの封筒には
もう1つの封筒の2倍の金額が入っている
選んだ封筒に1000円が入っていた場合
もう一方と交換したときの損得を
比と差で考える
(封筒のパラドックス4回目の動画youtube
のコメントでリクエストがありました)
---------------------------------------------
2封筒がA(500, 1000)の場合
---------------------------------------------
1000→500の交換となるため
500/1000 = 1/2倍(比の期待値)になる
500-1000 = -500(差の期待値)になる
交換すると損する
2封筒の期待値(500+1000)/2 = 750より
得ている1000は得している状態だからです
---------------------------------------------
2封筒がB(1000, 2000)の場合
---------------------------------------------
1000→2000の交換となるため
2000/1000 = 2倍(比の期待値)になる
2000-1000 = +1000(差の期待値)になる
交換すると得する
2封筒の期待値(500+1000)/2 = 750より
得ている500は損している状態だからです
---------------------------------------------
2封筒がA(500, 1000)とB(1000, 2000)の平均
---------------------------------------------
(500/1000 + 2000/1000)/2
= (500 + 2000) / 2000 = 2500/2000
= (2.5)/2 = 1.25倍
これは、500と2000という同時に存在しない
値を使用しているため意味のない数値です
同時に存在している場合は、下記で説明します
{(500-1000) + (2000-1000)}/2
= (-500 + 1000)/2 = 500/2 = +250
これも、500と2000という同時に存在しない
値を使用しているため意味のない数値です
この時点で、シミュレーションの各場合の
平均値は正しいのですが
全パターンの平均値には意味がない事が
分かります
同時に存在している場合は、下記で説明します
---------------------------------------------
4封筒A(500, 1000),B(1000, 2000)の場合
---------------------------------------------
2組のA(500, 1000),B(1000, 2000)から
無作為に1組選び、その中から1封筒を選ぶと
中身が1000だった場合
もう一方の封筒の中身はそれぞれ1/2の確率で
500か2000になりますので
上記のA,Bの平均値(比1.25倍と差+500)は意味を
持ち正しい値になります
各金額を選ぶ確率は1/4ずつなので
期待値(500+1000+1000+2000)/4 = 1125となり
得ている1000は損している状態ですので
交換した方が得だと分かります
この場合交換するときの期待値は
(1000/2 + 1000・2)/2 = (500+2000)/2
= 1250なので交換した方が得です
1000円は125損している状態なので
残りは125得している状態と予想できるので
交換すると+125-(-125) = +250となると
予想できます
交換するときの期待値1250は1000と比べて
比は1.25倍、差は+250になり
A(500, 1000)とB(1000, 2000)の場合の
平均と同じ値になります
つまりAとBの両方が用意されていて
1000円を選んだという限定した場合は
のみにしか成り立たない理屈です
---------------------------------------------
4封筒A,Bで1000を選んだと限定しない場合
---------------------------------------------
交換したときの損得
500を選んだ時
比は1000/500 = 2倍、差は1000-500=+500
1000を選んだ時(次の2通り)、
500に交換時、比は0.5倍、差は-500
1000に交換時、比は2倍、差は+1000
2000を選んだ時
比は1000/2000 = 0.5倍、差は1000-2000=-1000
これらの平均は
比は(2+0.5+2+0.5)/4 = 1.25倍
差は(500-500+1000-1000)/4 = 0
になります
現実には500,1000,2000のどれも
引く可能性がありますので
交換しても損得0になります
しかし、交換したとき、倍と半分が半々
の確率である金額(この場合1000)を
引いた時という、
条件を付ければ差の平均は+250
となり交換した方が得です
---------------------------------------------
6封筒A,B,Cの場合
---------------------------------------------
A(500, 1000),B(1000, 2000),C(2000, 4000)
交換したときの損得
500を選んだ時
比は1000/500 = 2倍、差は1000-500=+500
1000または2000だった時(次の4通り)、
1000→500の時、比は0.5倍、差は-500
1000→2000の時、比は2倍、差は+1000
2000→1000の時、比は0.5倍、差は-1000
2000→4000の時、比は2倍、差は+2000
2000を選んだ時
比は4000/2000 = 2倍、差は4000-2000=-2000
これらの平均は
比は(2+0.5+2+0.5+2+0,5)/6 = 1.25倍
差は(500-500+1000-1000+2000-2000)/6 = 0
になります
しかし、交換したとき、倍と半分が半々
の確率である金額(この場合1000か2000)を
引いた時という、
条件を付ければ差の平均は
(-500+1000-1000+2000)/4 = +1250
となりますが
これは1000と2000のどちらを引いたか
分かっていない場合で
分かった後は計算し直す必要があります
---------------------------------------------
結論
---------------------------------------------
1組の場合はもちろんn(有限個)組の封筒を
用意しても、交換したときの損得は0になる
交換したとき2倍か半分になる可能性がある
場合のみという条件を付けれは
交換したときの損得は0より大きくなり
交換した方が得です
交換すると半分になる確率が1の場合と
交換すると2倍になる確率が1の場合の
平均値は
手持ちが1000などと決定した後には
500(確率1)と2000(確率1)という同時には
あり得ない数値で計算することになるため
無意味な数値となり
シミュレーションの全平均値は
無意味な数値になります
500(確率0.5)と2000(確率0.5)ならOKですが
500(確率1)と2000(確率1)を含めると
全部の確率が3になりますので期待値は
計算できません
---------------------------------------------
空想実験(実現不可能な想像です)
---------------------------------------------
ここで上記結論のnを∞にすれば、
何を引いても
交換したとき2倍か半分になる可能性がある
場合になると思われますが
大きいほうは無限に大きくできますが
小さいほうは
次の2通り考えられます
1. 小さいほうは0で下限がある場合
お金なので0又は1が下限になります
中身が実数の場合
0.0000…01(0は∞個) = 0となり
0より小さい数値がないとすると
下限は存在して上限は存在しない
場合は、期待値は0~∞までの和
を∞として∞∞/∞=∞(lim省略)
とすれば
交換した方が得になりそうです
2. 小さいほうにも下限がない場合
0.0000…01(0は∞個) ≠ 0と
して、いくらでも小さい数が
存在するとすると
交換したとき2倍か半分になる可能性がある
場合を想像できそうです
よってこの場合も交換した方が
得になりそうです
∞組の封筒空想すると、何を引いても
交換した方が得という、現実では
ありえない結果になりました
しかし、この思考実験が間違っていて
∞の時も現実と同じ損得なしになる
という結果が存在するかもしれません
間違いがあるかもしれませんので
ご了承下さい
NL-BASICとnl30102.zip(enve007.bas)は
以下のリンクからダウンロードできます
Readme.txtを読んで遊んで下さい
下記リストをマウスで選択しCtrl+cでコピーし、
NL-BASICの画面でAlt+v(Ctrl+vではないので注意)
でプログラムを読込めます。
enve007.bas
100 '----------------------------------------------------------------------
110 ' 封筒のパラドックス(7回目) by ULproject for N88-BASIC
120 '----------------------------------------------------------------------
130 DEFDBL A-Z
140 RANDOMIZE VAL(RIGHT$(TIME$, 2))
150 CLS
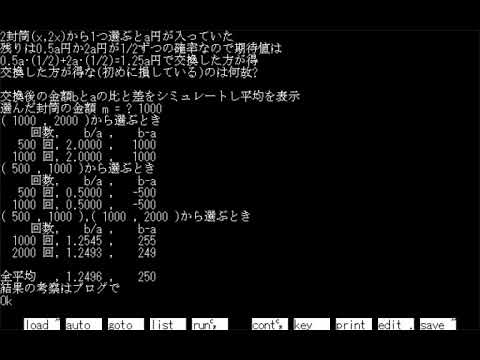
160 PRINT "2封筒(x,2x)から1つ選ぶとa円が入っていた"
170 PRINT "残りは0.5a円か2a円が1/2ずつの確率なので期待値は"
180 PRINT "0.5a・(1/2)+2a・(1/2)=1.25a円で交換した方が得"
190 PRINT "交換した方が得な(初めに損している)のは何故?"
200 PRINT
210 PRINT "交換後の金額bとaの比と差をシミュレートし平均を表示"
220 INPUT "選んだ封筒の金額 m = "; M
230 LOOP = 1000
240 M1 = M: M2 = M*2: GOSUB *ENVELOPE2: N1 = N: T1 = T: S1 = S
250 M1 = M/2: M2 = M: GOSUB *ENVELOPE2: N2 = N: T2 = T: S2 = S
260 '--- 2倍と半分は1/2の確率なので他の確率1に合わすため
270 '--- 試行回数を2倍にする
280 LOOP = LOOP * 2
290 M1 = M/2: M2 = M
300 M3 = M: M4 = M*2: GOSUB *ENVELOPE4: N3 = N: T3 = T: S3 = S
310 PRINT
320 N = N1 + N2 + N3
330 T = T1 + T2 + T3
340 S = S1 + S2 + S3
350 PRINT USING "全平均 , #.#### , ######"; T/N, S/N
360 PRINT "結果の考察はブログで"
370 END
380 '--- 2封筒(選んだ金額が上限又は下限のとき)
390 *ENVELOPE2
400 PRINT "("; M1; ","; M2; ")から選ぶとき"
410 PRINT " 回数, b/a , b-a"
420 T = 0 '--- 比
430 S = 0 '--- 差
440 N = 0 '--- 試行回数
450 WHILE N < LOOP
460 A = M1
470 B = M2
480 IF A <> M THEN SWAP A, B
490 T = T + (B / A)
500 S = S + (B - A)
510 N = N + 1
520 GOSUB *DISPLAY
530 WEND
540 RETURN
550 '--- 4封筒(交換時2倍と半分が半々で起こる場合)
560 *ENVELOPE4
570 PRINT "("; M1; ","; M2; "),("; M3; ","; M4; ")から選ぶとき"
580 PRINT " 回数, b/a , b-a"
590 T = 0 '--- 比
600 S = 0 '--- 差
610 N = 0 '--- 試行回数
620 WHILE N < LOOP
630 A = M1
640 B = M2
650 IF RND(1) < 0.5 THEN A = M3: B = M4
660 IF A <> M THEN SWAP A, B
670 T = T + (B / A)
680 S = S + (B - A)
690 N = N + 1
700 GOSUB *DISPLAY
710 WEND
720 RETURN
730 '--- Display
740 *DISPLAY
750 IF N MOD (LOOP\2) THEN RETURN
760 PRINT USING "###### 回, #.#### , ######"; N, T/N, S/N
770 RETURN