アイスミルクティーじゃなかったのかよとか、なんでいきなし英語なんだよと言ったツッコミはなしで^^;
かなりどうでもいいですが、今年からLupiciaの2nd flushのパッケージの色が青になったみたいですね

これまでは他の紅茶と同じく赤だったのに………2nd flushは紅茶の中でも最高級品 なので、プレミア感をつけたってとこでしょうか。
なので、プレミア感をつけたってとこでしょうか。

気づいた方はあまりいないと思いますが、携帯機種変のためカメラ変わりました(実は前回も)。画素数は増えてるんですが、なんかイマイチ。てかプレゼントでデジカメもらったので、今度からそれ使うか…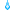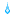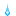
今回はほぼ開封直後(2回目)です!今までの投稿だとなぜか「もうそろそろ茶葉なくなるよーー(>_<)」てのが多かった気がします。
初開封だと、どれくらいの濃さや時間で入れたらよいものか判然としないのですが、一度飲んでしまえば大体わかります。したがって2回目が一番おいしい!…こともある(気分とかにもよるかなー )
)
今回も、1回目はちょっと薄くてイマイチだった(たぶんうちの彼女に飲ませてもわかりませんがww)。味見をしたとき「あと一息かな?」ってあたりで淹れるのが鉄則、ではあるんですが、この「あと一息」がどれくらいかがちょっと見極めにくい。2回目は30秒弱追加したら、ちょうどよい濃さになりました。
最近は今まで以上にジャンピングを意識して、すべての茶葉を表面に集めるつもりで淹れてるんですが、なかなか難しいですね。十分に沸騰させたお湯を高い位置から勢いよく注ぐ、これはできてるつもりなのですが…
肝心のお茶ですが、さすが2ndは香気の量が半端ない
基本的に高級な茶葉というのはそれなりにおいしいです、味も香りも。
ただ、それが単純な比例関係であるかは怪しい。むしろ値段は指数関数的に上がるのに対して、味の絶対的・総合的な尺度は無理関数的にしか上がらない気がするので、コストパフォーマンスは悪いかも。それでも飲みたくなるのはもはやバカかもしれませんね(苦笑)
かなりどうでもいいですが、今年からLupiciaの2nd flushのパッケージの色が青になったみたいですね


これまでは他の紅茶と同じく赤だったのに………2nd flushは紅茶の中でも最高級品
 なので、プレミア感をつけたってとこでしょうか。
なので、プレミア感をつけたってとこでしょうか。
気づいた方はあまりいないと思いますが、携帯機種変のためカメラ変わりました(実は前回も)。画素数は増えてるんですが、なんかイマイチ。てかプレゼントでデジカメもらったので、今度からそれ使うか…
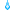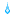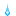
今回はほぼ開封直後(2回目)です!今までの投稿だとなぜか「もうそろそろ茶葉なくなるよーー(>_<)」てのが多かった気がします。
初開封だと、どれくらいの濃さや時間で入れたらよいものか判然としないのですが、一度飲んでしまえば大体わかります。したがって2回目が一番おいしい!…こともある(気分とかにもよるかなー
 )
)今回も、1回目はちょっと薄くてイマイチだった(たぶんうちの彼女に飲ませてもわかりませんがww)。味見をしたとき「あと一息かな?」ってあたりで淹れるのが鉄則、ではあるんですが、この「あと一息」がどれくらいかがちょっと見極めにくい。2回目は30秒弱追加したら、ちょうどよい濃さになりました。
最近は今まで以上にジャンピングを意識して、すべての茶葉を表面に集めるつもりで淹れてるんですが、なかなか難しいですね。十分に沸騰させたお湯を高い位置から勢いよく注ぐ、これはできてるつもりなのですが…
肝心のお茶ですが、さすが2ndは香気の量が半端ない

基本的に高級な茶葉というのはそれなりにおいしいです、味も香りも。
ただ、それが単純な比例関係であるかは怪しい。むしろ値段は指数関数的に上がるのに対して、味の絶対的・総合的な尺度は無理関数的にしか上がらない気がするので、コストパフォーマンスは悪いかも。それでも飲みたくなるのはもはやバカかもしれませんね(苦笑)

 )。
)。