『心理統計法』の印刷教材では「3囚人問題」の説明がわかりにくいので
私が説明するならこのようにするというものを紹介しておきます![]()
【問】
ある監獄では、罪状はいずれも似たりよったりである3人の死刑囚A、B、Cがそれぞれ独房に入れられている。3人まとめて処刑される予定であったが、1人が恩赦になって釈放され、残り2人が処刑されることとなった。だれが恩赦になるか知っている看守に「私は助かるのか」と囚人が聞いても看守は答えない。そこでAは「BとCのうち少なくとも1人処刑されるのは確実なのだから、2人の中で処刑される1人の名前を教えてくれても私についての情報を与えることにはならないだろう。1人を教えてくれないか」と頼んだ。看守はAの言い分に納得して、「囚人Bが処刑(dead)される」と答えた。それを聞いたAは「これで自分が助かる(alive)確率は 1/3 から 1/2 に増えた」と喜んだ。実際には、この情報を得た後、Aの釈放される確率は増えたのか?
少し話が込み入っているので、まず注目している確率を確認しておくと
Aが生き残る確率
です![]() この確率が
この確率が
Bは処刑される
という「情報」を得ることによって変化するのか![]()
がこの問題の趣旨になります![]()
ここで「情報」を得る前のAが生き残る確率を事前確率
「情報」を得た後のAが生き残る確率を事後確率といいます![]()
印刷教材では式がズラズラ並んでいて、とてもわかりにくいけど
確率を考えるときには図を描いて面積で考えるのがいいです![]()
情報を得る前は、A自身がそう思っているように
A、B、Cが生き残る確率はそれぞれ 1/3 と考えましょう。
これを図を使って表すと下のようになりますね![]()
注目しているのはAが生き残る確率なので
事前確率 = 1/3
です![]()
ここで看守がAに対して「Bは処刑される」「Cは処刑される」の
どちらの情報を伝えるのか、それぞれの場合で見ていきましょう![]()
・Aが生き残る場合
この場合にはBとCが処刑されるので、看守は
「Bは処刑される」「Cは処刑される」どちらを伝えてもいいです![]()
そこで、それぞれの確率を 1/2 で伝えることにすると
図はさらに次のように書くことができます![]()
・Bが生き残る場合
この場合にはAとCが処刑されるので、看守は自動的に
「Cは処刑される」と伝えることになります![]()
したがって図は下のように書き加えることができます![]()
・Cが生き残る場合
この場合にはAとBが処刑されるので、看守は自動的に
「Bは処刑される」と伝えることになります![]()
したがって図は下のように書き加えることができます![]()
ここまで来たらいよいよ「Bは処刑される」という情報を得る段階です![]()
この情報を得ることによって、一部の可能性が消えますね![]()
「Cは処刑される」と伝えている部分です![]()
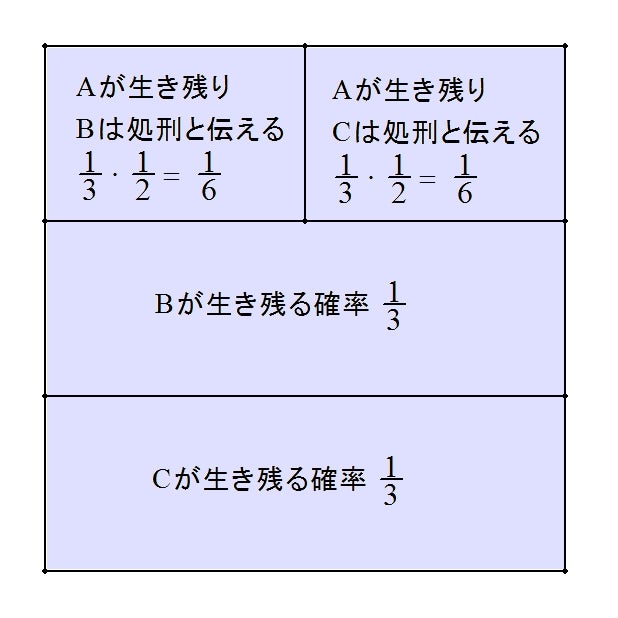
なので図は次のように一部だけが残ることになります![]()
起こり得る確率を全部足して 1 になる必要があるので、残った
「Aが生き残りBは処刑と伝える」と「Cが生き残りBは処刑と伝える」を
足して面積が 1 になるように補正(正規化)します![]()
この結果、Aは「Bは処刑される」という情報を得た後も
生き残る確率は変化せず 1/3 のままとなります![]() つまり
つまり
事後確率 = 1/3
となるわけです![]()
これが多くの人の直観に反する結果となっているので
「3囚人問題」は、よく似た「モンティ・ホール問題」とともに
有名な数学ネタになっています![]()
(ここからちょっと難しいよ![]() )
)
ここで、Aが生き残る場合について
看守が「Bは処刑される」「Cは処刑される」と伝える確率が
それぞれ 1/2 の確率ではないとしてみましょう![]()
急に数学っぽくなりますが「Bが処刑される」と伝える確率を p、
「Cは処刑される」と伝える確率を 1-p と考えてみるのです![]()
すると最後から2番目に示した図は下のようになります
これを正規化することによってAが生き残る事後確率 q は
と計算することができます![]()
さっきは p = 1/2 だったので事後確率は 1/3 でした![]()
次に p の分布を考えてみましょう![]()
この部分がわかりにくいんだけど確率 p の確率分布です![]()
例えば成人女性の平均身長の分布といえば
こんな形(ほぼ正規分布)になることが知られているけど
これと同じように p についても分布を考えちゃおうってこと![]()
もちろん p は確率なので 0~1 の範囲しか値しかとらず
その範囲で一様分布に従うと仮定します![]() つまり
つまり
確率 p が![]() のような分布をとるってことです
のような分布をとるってことです![]()
p がこのような分布をとるときに q はどのような分布 g(q) をとるか![]()
がここで考えたい最終的な結論になります![]()
この求め方は分布関数を使って求める方法とそうでない方法と
2通りあるんですが…どちらも結局「微分」を使います![]()
(ここからガチガチの数学です![]() )
)
もしも p が p ~ p + Δp の範囲にあったときに
q が q ~ q + Δq の範囲にあったとしてます![]()
つまり p については
このようにある微小範囲にあるとします![]()
求めたい q の分布 g(q) はわからないけど
q は p の関数なので自動的に連動して
仮に上のような範囲を動くことになりますね![]()
ここで p と q は関数でつながっているので
この2つのピンクの面積(確率)は等しくなる必要があり
Δp と Δq が十分に小さいと考えれば
2つのピンクの部分をともに長方形と見て計算すると
という式が得られます![]()
ここで両辺を Δp で割って Δp → 0 (Δq → 0) の極限をとれば
という微分を用いた式で書けることになります![]()
いま f(p) = 1 はわかっていて、数Ⅲの知識を使う必要があるけど
なので上の式に代入してあげれば
が得られます![]()
最後に p と q の関係式を式変形してあげれば
なのでこれを上の g(q) の式に代入すれば印刷教材の最後にある
となるんです![]()
なお p = 0 のとき q = 0, p = 1 のとき q = 1/2 になるので
0 ≦ q ≦ 1/2 の範囲をとりグラフにすると
印刷教材の最後と同じものになりますね![]()
最後の方はちょっと難しかったかもしれないけど
「事前確率」と「事後確率」の意味が伝わればいいなぁ![]()