ピタゴラスの定理【序初】目次/概要プレーン敵督
ピタゴラス数
a2 + b2 = c2 を満たす自然数の組 (a, b, c) をピタゴラス数またはピタゴラスの三つ組数 (Pythagorean triple) という。特に、a, b, c が互いに素であるピタゴラス数 (a, b, c) を原始的 (primitive) あるいは素 (prime) であるといい、そのようなピタゴラス数は原始ピタゴラス数 (primitive Pythagorean triple) などと呼ばれる。全てのピタゴラス数は、原始ピタゴラス数の正の整数倍により得られる。
ピタゴラス数 (a, b, c) が原始的であるためには、3つのうち2つが互いに素であることが必要十分である。
ピタゴラス数の性質
2つの整数mとn(m>n≧1)を基にピタゴラス数(a,b,c)を生成できることを示した図。単一の黄色の長方形および正方形の面積はいずれも{\displaystyle m^{2}n^{2}}となっている。
色付きの正方形群で三辺の長さが整数の直角三角形を表した例。正方形の合計数は図中右上のように1つの長方形内に余白なく収まるものとなっている。
ピタゴラス数を面積及び長さの比で表した図。青は{\displaystyle m^{2}-n^{2}}、緑は{\displaystyle 2mn}、赤は{\displaystyle m^{2}+n^{2}}を表現している。右上の矢印の先で青の長方形の右の辺の延長線並びに赤と青の円弧が交差していることで、面積及び長さの比が直角三角形の三辺の比として成り立っていることが確認できる。
数1に相当する長さを定めた上でピタゴラス数の関係を長さで表した図。ピタゴラス数を表現する長さが直角三角形(桃色)の三辺として成り立っていることが確認できる。(赤矢印が示す交点一致)
自然数の組 (a, b, c) が原始ピタゴラス数であるためには、ある自然数 m, n が
- m と n は互いに素
- m > n
- m − n は奇数
を満たすとして、
- (a, b, c) = (m2 − n2, 2mn, m2 + n2) or (2mn, m2 − n2, m2 + n2)
であることが必要十分である。上記の (m, n) は無数に存在し、2mn は重複しないから、原始ピタゴラス数は無数に存在する。これにより、すべての原始ピタゴラス数を重複なく見つけ出すことができる。
例えば
- (m, n) = (2, 1) のとき (a, b, c) = (3, 4, 5)
- (m, n) = (3, 2) のとき (a, b, c) = (5, 12, 13)
- (m, n) = (4, 1) のとき (a, b, c) = (8, 15, 17)
である。
原始ピタゴラス数 (a, b, c) について、次のような性質も成り立つ。
- a または b は 4 の倍数
- a または b は 3 の倍数
- a または b または c は 5 の倍数
また、一般のピタゴラス数 (a, b, c) に対して、S = 12ab(直角三角形の面積)は平方数でない。
直角三角形の三辺の長さを整数とするための調整
直角三角形の三辺の長さを整数とするための調整の図
直角三角形の三辺の長さを整数とするための調整の図において、赤の正方形の面積から青の正方形の面積を差し引いた残りの面積を互いに合同な黄の長方形4枚で占めている。
黄の長方形の長辺と短辺の長さが整数であれば、
- 赤の正方形の辺の長さは黄の長方形の長辺と短辺の和
- 青の正方形の辺の長さは黄の長方形の長辺と短辺の差
となり、いずれも整数として表せることになる。
また、黄の長方形の面積を整数の二乗で表せれば、黄の長方形4枚分の面積に等しい緑の正方形の辺の長さも整数で表すことができる。
なおかつ、二つの正方形(緑と青)の面積の和が別の正方形(赤)の面積となることにもなり、この場合、三つの正方形の各辺の長さを用いて直角三角形(桃色)を作れることになる。
ただし、黄の長方形は当然正方形となってはならず(長辺と短辺の差によって青の正方形を作る必要がある)、互いに異なりながらその積が整数の二乗となる2つの数を黄の長方形の幅と高さに割り当てる必要がある。
それを実現する方法の一つとして、黄の長方形の幅と高さをそれぞれ異なる整数の二乗とする方法がある。
図では、数1の長さを定めた上で整数m,n(m>n≧1)の長さも設定し、それぞれの二乗を黄の長方形の辺の長さにしている。
(緑の正方形の辺の長さは {\displaystyle 4m^{2}n^{2}} の正の平方根 {\displaystyle 2mn} となる。)
青、緑、赤の各正方形の辺の長さをa,b,cとすると、
- {\displaystyle a=m^{2}-n^{2}}
- {\displaystyle b=2mn}
- {\displaystyle c=m^{2}+n^{2}}
となり、それぞれ整数であり、{\displaystyle a^{2}+b^{2}=c^{2}} が成り立つので、a,b,cを三辺の長さとする三角形(桃色)は直角三角形となる。
Jesmanowicz 予想
1956年に Jesmanowicz が以下の予想を提出した。
(a, b, c) を原始ピタゴラス数、n を自然数とする。x, y, z が
- {\displaystyle (an)^{x}+(bn)^{y}=(cn)^{z}}
で自然数解を持つには、
- {\displaystyle x=y=z=2}
であることが必要である。
一般化
角の一般化
詳細は「余弦定理」を参照
- c2 = a2 + b2 − 2ab cos C
はピタゴラスの定理を C = π2 = 90° → cos C = 0 の場合として含む。 つまり、第二余弦定理はピタゴラスの定理を一般の角度について拡張した定理になっている。
指数の一般化
詳細は「フェルマーの最終定理」を参照
指数の 2 の部分を一般化すると
- an + bn = cn
となる。n = 2 の場合は自明でない(つまり a, b, c のいずれも 0 でない)整数解は実質原始ピタゴラス数であり、無数に存在するが、n ≥ 3 の場合には自明でない整数解は存在しない(詳細はフェルマーの最終定理を参照)。
次元の一般化
詳細は「en:De Gua's theorem」を参照
3次元空間内に平面があるとき、その閉領域 S の面積は、yz 平面、zx 平面、xy 平面への射影の面積 Sx, Sy, Sz を用いて
- {\displaystyle S^{2}={S_{x}}^{2}+{S_{y}}^{2}+{S_{z}}^{2}}
と表される。これは高次元へ一般化できる。

 となっている。
となっている。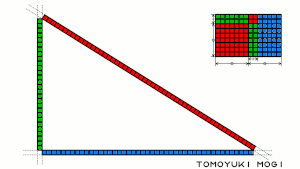

 、緑は{\displaystyle 2mn}
、緑は{\displaystyle 2mn} 、赤は{\displaystyle m^{2}+n^{2}}
、赤は{\displaystyle m^{2}+n^{2}} を表現している。右上の矢印の先で青の長方形の右の辺の延長線並びに赤と青の円弧が交差していることで、面積及び長さの比が直角三角形の三辺の比として成り立っていることが確認できる。
を表現している。右上の矢印の先で青の長方形の右の辺の延長線並びに赤と青の円弧が交差していることで、面積及び長さの比が直角三角形の三辺の比として成り立っていることが確認できる。

 の正の平方根 {\displaystyle 2mn}
の正の平方根 {\displaystyle 2mn}


 が成り立つので、a,b,cを三辺の長さとする三角形(桃色)は直角三角形となる。
が成り立つので、a,b,cを三辺の長さとする三角形(桃色)は直角三角形となる。

