今日母が指導している塾で、3÷0や7÷0と言った0で割る計算問題を扱ったらしい。
そしてその模範解答が0だったのが、疑問で生徒に対してもうまく説明できなかったそうだ。
自分もその話を聞いた時には、「は？そもそもそんなこと考えること自体おかしいだろ
？」と思ったので、以降に数学科卒の私の観点から0で割ることの意味を掘り下げていく
テーマ:0で割る意味を探ろう！
0.前置き(小学生レベル)
まずは、普通の割り算を例とともに確認する。
(ex.1)
6 ÷ 2 = 3
これは次のように物を用意して考えると分かりやすい。
これは木箱の中に赤球が6個入っているイラストですね
このイラストを基に6÷2を考えると、、、
このことから、箱の中が空になるように2個ずつ何回分けることができるのかその回数こそが6÷2の解に対応しているといえます。
したがって、6÷2=3となるわけですね
1. 0で割ることの意味(中学生レベル)
さて、ここから0で割る操作について見ていこう。
(ex.2)
7 ÷ 0 = ?
ここでex.1を振り返ってみる↩️
6 ÷ 2 = 🔸
という風に求める部分を🔸で表してみる。
これを両辺2倍して、
6 = 🔸 × 2
入れ換えれば、
🔸 × 2 = 6
となる。
そうすると同じことを7 ÷ 0 = ?にもやればなんかわかるのでは🤔となりますよね。なのでそれも下にやってみると、、、
7 ÷ 0 = 🔹
7 = 🔹 × 0 ・・・(＊)
🔹 × 0 = 7
となる。
さて、このような数🔹は存在するでしょうか
・・・
結論存在しません
では、他の数を割るとどうでしょうか？
6 ÷ 0 = ？
-2 ÷ 0 = ?
これらも上と同様の操作で解は存在しないことがわかります
では、どんな数も0で割る場合、解が無かったんだ
と結論づけて良いのでしょうか
いいんじゃない
と思う方もいるでしょう。しかし、そうしてしまうのはちょっと早計です
実は1つだけ例外があるんです
それが次の例に示すものになります。
(ex.3)
0 ÷ 0 = ?
今までと同様の操作を行いましょう
0 ÷ 0 = 🔹
0 = 🔹 × 0
🔹 × 0 = 0
さて、この場合は🔹にどんな数が入るか考えると、、、
なんと今までと違い全ての実数が当てはまります
このように0で割られる数によって解が異なってしまいます
結論
a ÷ 0 = (解なし) (a ≠ 0)
a ÷ 0 = (全ての実数) (a= 0)
となるわけですねちなみに上の場合を不能,下の場合を不定と言ったりします
ただし、一定数の人は納得いかない部分があったのではないでしょうか
それはどこかというと(＊)の部分です。これは自然にやっていますが、0が分母にあって0をかけて消しあっちゃったよという操作をしているんですよね。
・・・
これってよく考えたらまずくないですか
「ん？どこが。」と思った人もいると思います。
それは、結論を得る前に0で割るということを認めて使っているということです
認めたいことを説明するのに、それ自体を説明に含めるのはおかしいでしょうという話です。
・・・
じゃあどうすればいいのとなった方は次の節を見れば解決します
2.そもそも0で割れない(小学生レベル)
はいここからは1.で解決しなかった部分を掘り下げます。
まず、もともと割り算というのは、逆数をかけるということなんです。だから、ex.1だと2で割ることが1/2をかけるということを実は意味していたということですね
これを踏まえて、もう一度(ex.1)を見直すと、
6 ÷ 2 = 🔸
6 × (1/2) = 🔸
6 × (1/2) ×2= 🔸 ×2
🔸 × 2 = 6
となるということですね
つまり、ex.1から続けている計算が成り立つには逆数の存在が言えてないとダメだったのです
じゃあ0の逆数があるのかと考えると、、、
結論無いですね(なぜなら,0にかけて1になる数は存在しないから)
はい。よって0で割ることは、割り算の定義に基づいて考えるとそもそも定義不可能だったということですね
3.オマケ(極限について)(高校生レベル)
おまけとして極限を使って0で割る話について議論したいと思う
さて,そうすると lim(x → 0) (1/x)という極限が存在するか考えればいいということになるが,果たして存在するだろうか、、、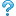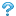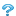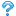
これは右側極限と左側極限が一致することが確認できれば良いだろう.でも実際に手を動かすと、、、
このようになり,近づけ方によって結果は異なってしまう😳
したがって, lim(x → 0) (1/x) = (存在しない)という風に結論付く訳である
以上より,極限を使うことでも0で割れないことを説明することができました
時間があれば,geogebra等の関数グラフを作るアプリを使って反比例のグラフを書いて視覚化してみるのも良いですね
はい.今回はこの程度で話は留めますが,結論0で割ると0というのは,数学的根拠は全く無いものだったというわけですね
おそらく定義できないこと自体を説明することは現時点では難しいと解答作成側が考えて,とりあえず何も無いという意で0を用いたのだと思います.
(追記)2.の話は厳密に言うと体の公理と関連があるので,興味がある人はこの機会に調べてみるとより理解が深まると思います