四則演算だけで微分を解説します
1.1微分を体験する
まず、速度の例を用いて微分を体験してもらいます。
ある学者、コメ太郎くんは、坂道を転がるおにぎりの進む距離と時間との関係を実験で次のように結論しました。
s=2t²
(sはおにぎりが進む距離、tは時刻です)
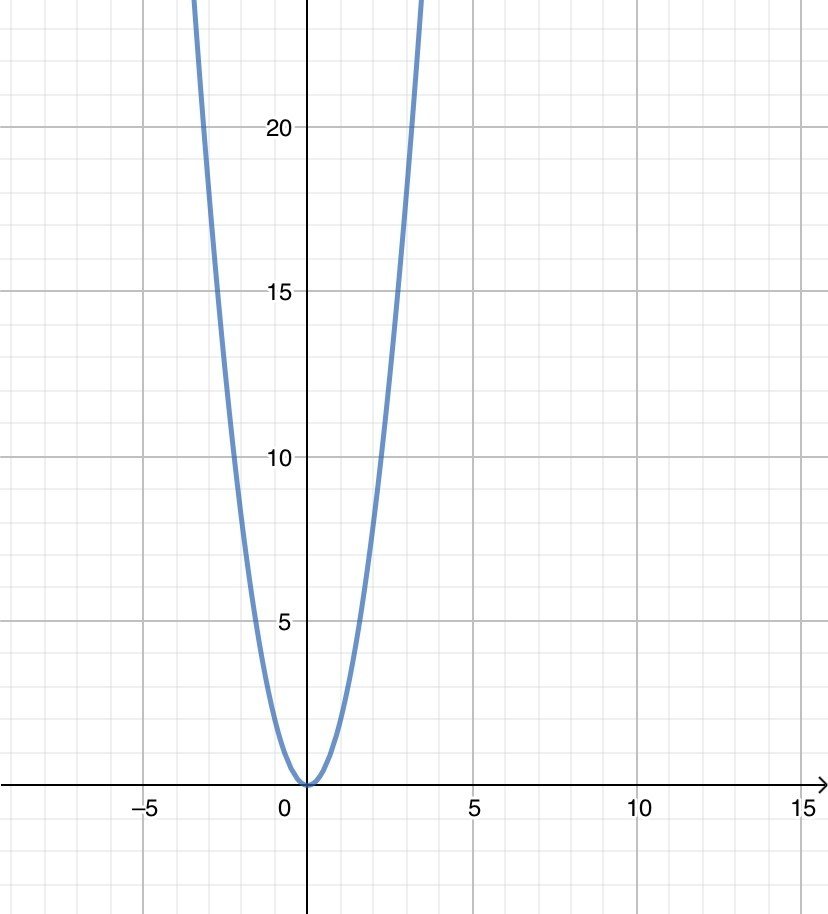
(☝s=2t²のグラフ 横軸がt 縦軸がs)
ある時間の間におにぎりが進んだ距離を求めてみましょう。(例えば、t=1からt=5の間に進んだ距離、t=1からt=16の間に進んだ距離など)。しかしいちいち、tの値を変えるのは面倒なのである正の数hをもってきます。このhを時間の幅としてt=1からt=1+hの間におにぎりが進んだ距離を求めてみましょう。(そうすると後でhに好きな数字を入れれば、それに対応した距離が求まります。)
求めると
t=1 のとき s=2
t=1+h のとき s=2(1+h)²
なので、t=1からt=1+hの間におにぎりは
2(1+h)²−2=2(1+2h+h²)−2
=4h+2h²
だけ進みますね。
では次に、1秒間にはどれだけ進むのか求めます。時間hの間に進んだ距離を時間hで割ると、1秒間で進んだ距離になりますね。(例えば、3秒間で6m歩いた時、1秒間では2m歩いています。)
ということで求めると、1秒間におにぎりは
・・・①
だけ進みます。これはt=1からt=1+hの間の”平均速度”といいます。例えば、h=5のときは、t=1からt=6の間の平均速度は14となりますね。
時間間隔hで平均速度を求めました。でも、s=2t²のグラフは横軸tが大きくなるにつれてだんだん勾配が急になっています。つまり、tの間隔が同じでも最初の方のtではsの値も小さい(進む距離が小さい)が、後の方のtではsの値も大きい(進む距離が大きい)ことが分かります。ということはtの場所によって同じ時間をかけても進む距離が異なる=速さが異なるわけです。例えば、家を出て高速道路に乗って途中にパーキングエリアで休憩していろいろして目的地に着いた。家から目的地までの距離は300㎞、家を出て目的地までにかかった時間は6時間。この場合の平均速度は時速50㎞になるわけですが、常に時速50㎞でいたわけではないですよね。高速道路で時速100㎞のときもあれば、パーキングエリアで休憩したので時速0㎞のときもあったわけです。(先ほど導いた平均速度は、この時速50㎞の意味だったのです。)
時速100㎞とか時速0㎞とかはその時のメーターに映し出されている、その”瞬間”の速さなのです。ということでおにぎりの平均速度が分かったところで、次は坂道を転がるおにぎりの瞬間の速さを求めてみましょう
このラインより上のエリアが無料で表示されます。
具体的に、上でt=1を基準にして平均速度を出してきたので、ここもt=1の瞬間の速さを出します。
どうするかというと、t=1+hをt=1に近づけます。言い換えるとhをだんだん0に近づけるということです。hを限りなく0にしていくと、
h=0.00000000.......となり、t=1+0.00000000000…となって、もはやhは0に、tは1になります。
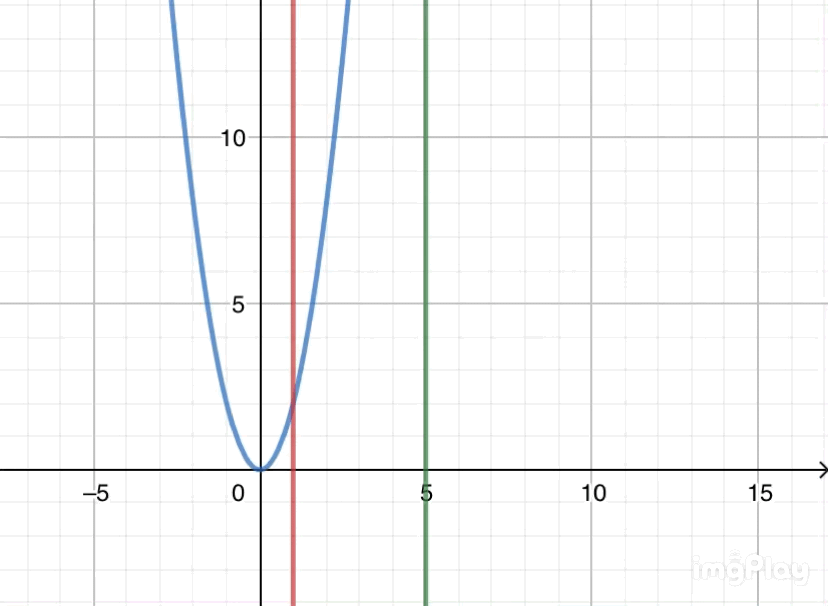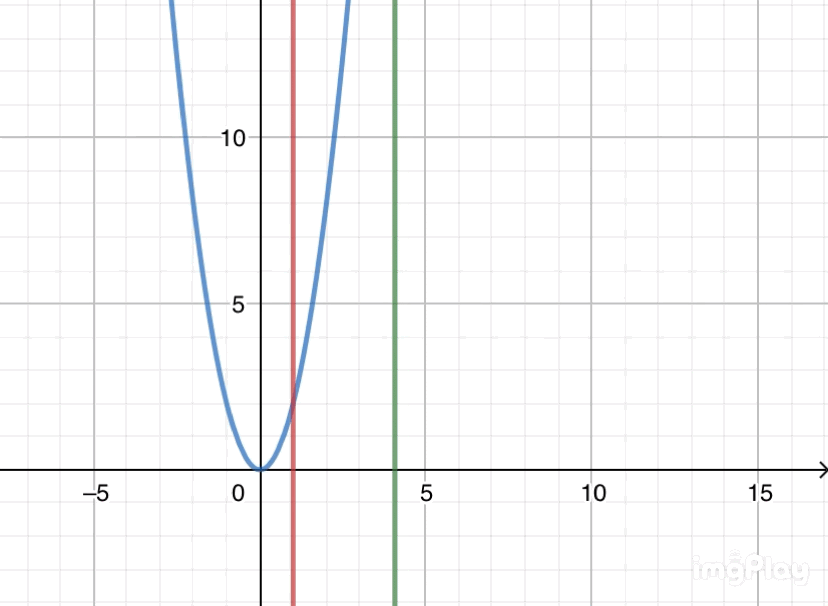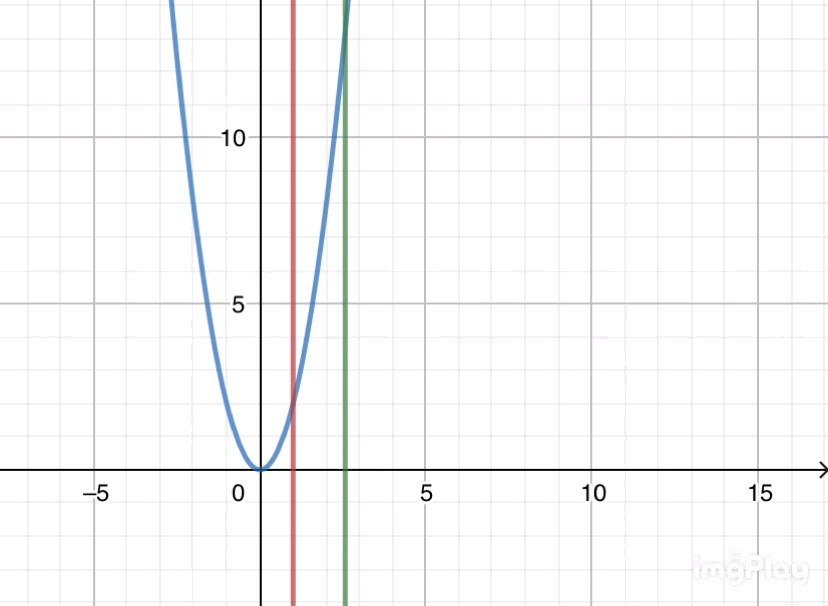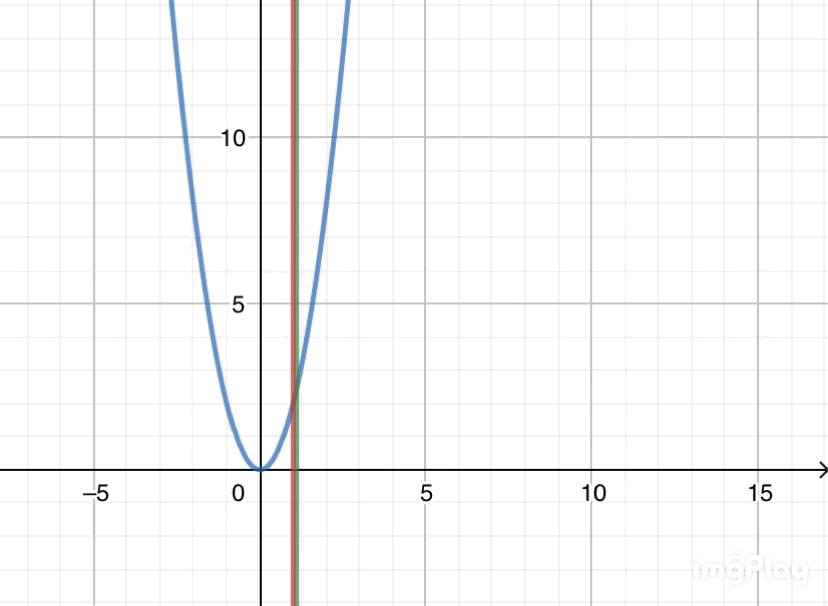
(☝赤線がt=1、緑線がt=1+h。t=1+hがt=1に近づく様子)
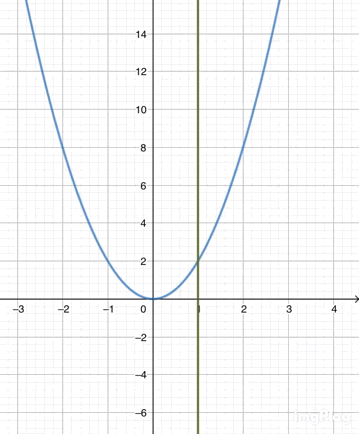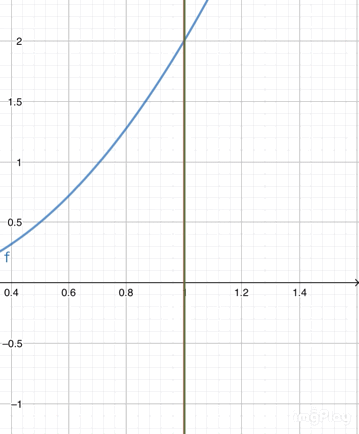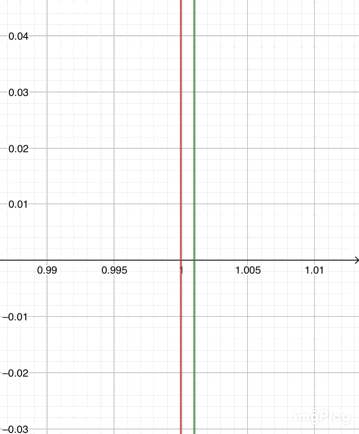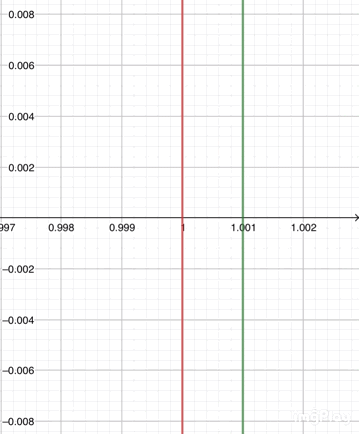
(☝t=1+hがt=1に近づいた、つまりhが限りなく0に近づいた時の様子。と言ってもh=0.01で0が2つ程度。hをほぼ0にできる意味が分かったと思う。)
整理します。
t=1からt=1+hで進んだ距離 → s=2(1+h)²−2=4h+2h²
t=1における瞬間速度 → 4+2・0=4 (h→0)
実はもうここまでで微分という操作をやっています。それはどこかというと、hを限りなく0に近づけて、瞬間速度を出した時。この操作が微分なのです。用語で書くと、関数s=2t²のt=1における微分は4である、となります。
ここまでの一連の流れを書きます
s=2t² におけるt=1からt=1+hの間の平均速度は
t=1での瞬間速度は 4+2h→4 (h→0)
お分かりの通り、まず平均速度を求めて瞬間速度を出しました。微分も同じです。
1.2微分とは何なのか?
ここまでで具体例を用いた微分の体験でした。結局、微分とは何かというとそれは“変化率”です。自然科学に限らず、世の中では対象となるモデルの変化率を求めることが大変重要なのです。物体の時間に関する位置の変化率(=速度)、製品の製造数に関する費用の変化率(=限界費用)、時間に関する反応物質濃度の変化率(=反応速度)などなど。